Written by Carlos Requena
on 

[BITCOIN] Keys and Addresses

"Our virtues and our failings are inseparable, like force and matter. When they separate, man is no more." --Nikola Tesla.


You may have heard that Bitcoin is based on cryptography, which is a branch of mathematics used extensively in computer security. Cryptography means “secret writing” in Greek, but the science of cryptography encompasses more than just secret writing, which is referred to as encryption. Cryptography can also be used to prove knowledge of a secret without revealing that secret (digital signature), or prove the authenticity of data (digital fingerprint). These types of cryptographic proofs are the mathematical tools critical to bitcoin and used extensively in bitcoin applications.

Ironically, encryption is not an important part of bitcoin, as its communications and transaction data are not encrypted and do not need to be encrypted to protect the funds. mastering bitcoin

ECDSA (‘Elliptic Curve Digital Signature Algorithm’) is the cryptography behind private and public keys used in Bitcoin. It consists of combining the math behind finite fields and elliptic curves to create one way equations, meaning you can choose your private key “Pick a number between 1 and \(2^{256}\).” and easily calculate your public key (some other number). However, You can not take the public key and easily calculate their private key. In fact, for Bitcoin it would take trillions of computers trillions of years of continuous guessing of different private keys to figure out which one creates a given public key. How does ECDSA work in Bitcoin

Elliptic curve cryptography (ECC)

Elliptic curve cryptography (ECC) is based on the discrete logarithm problem that is based on elliptic curves over finite fields (Galois fields). The main benefit of ECC over other types of public key algorithms is that it needs a smaller key size while providing the same level of security as, f or example, RSA.

An elliptic curve will simply be the set of points described by the equation:

\[\displaystyle y^{2} \ =\ x^{3} \ +\ ax\ +\ b\ where\ 4a^{3} \ +\ 27b^{2} \ \neq \ 0\]

(this is required to exclude singular curves) The equation above is what is called Weierstrass normal form for elliptic curves.

If we want to explicitly take into account the point at infinity, we can refine our definition of elliptic curve as follows:

\[\left\{( x,y) \ \in \mathbb{R}^{2} \ |\ y^{2} =x^{3} +ax+b,\ 4a^{3} +27b^{2} \neq 0\right\} \ \cup \ \{0\}\]

Algebraic addition

Algebraic formulae are constructed to efficiently compute the geometric arithmetic.

Adding distinct points P and Q

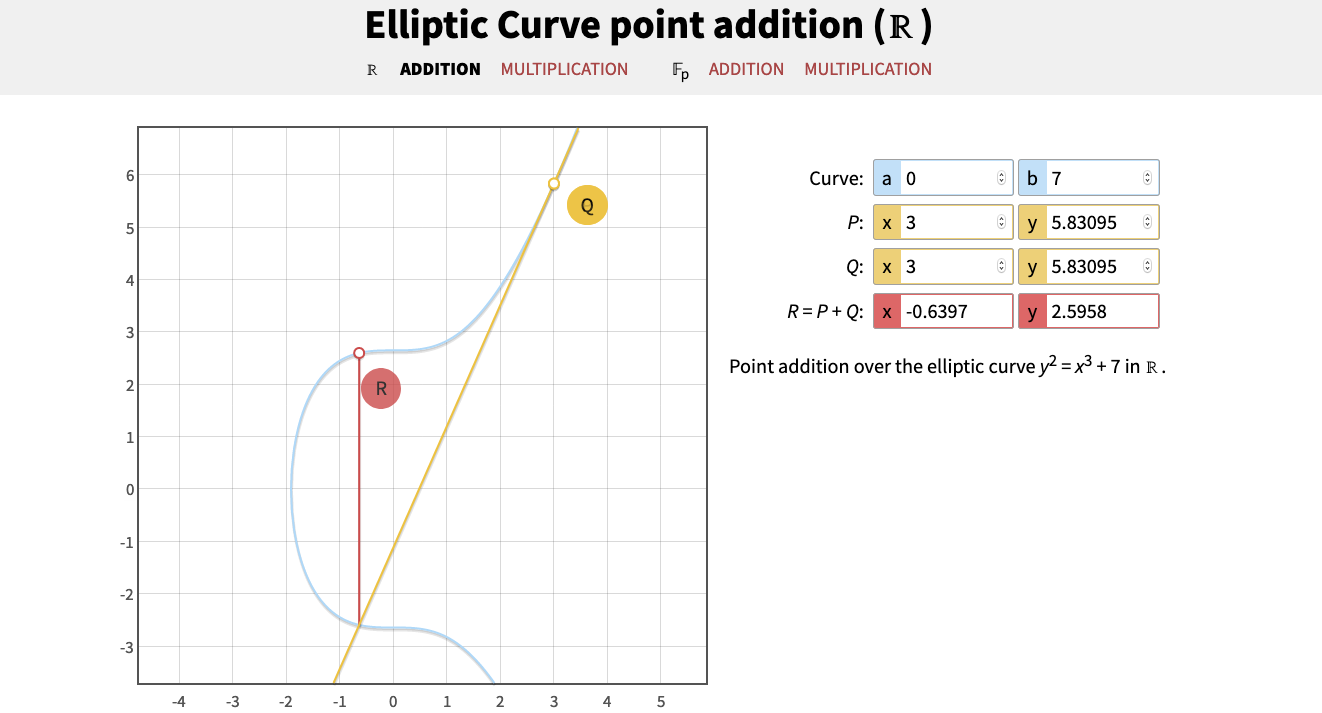
\[\begin{array}{l} When\ P=({X_p},{Y_p}) \ and\ Q=({X_q},{Y_q}) \ and \ they \ are \ not \ negative \ of \ each \ other \\ P + Q = R \\ {X_r}= m^{2} − {X_p} - {X_q} \\ {Y_r} = -{Y_p} + m({X_p} - {X_r}) \\ where \ m= \frac { ({Y_p} - {Y_q}) } { ({X_p} - {X_q}) } \\ \end{array}\]

Note that m is the slope of the line through P and Q.

Doubling the point P

When P and Q share the same position (X and Y wise), addind two points (P and Q ) that share the same location is called “Doubling the point P” also referred as adding a point to itself.

\[\begin{array}{l} When\ {Y_p} \neq 0,\ 2P\ =\ R\ \\ {X_r} = m^{2} − {2X_p} \\ {Y_r} = -{Y_p} \ +\ m({X_p} \ -\ {X_r}) \\ Where\ m\ =\ \frac{\left( 3Xp^{2} \ +\ a\right)}{( 2Yp\ )} \\ m \ is \ the \ slope \ of \ the \ tangent \ line \ when \ point \ P \ and \ point \ Q \ are \ or \ tend \ to \ be \ equal, \\ then \ deriving \\ \frac{\text{d}y(x)}{\text{d}x}(\sqrt{x^{3} + 7 + a}) = \frac{\left( 3X^{2} \ +\ a\right)}{( 2Y\ )} \\ \end{array}\]

Recall that a is one of the parameters chosen with the elliptic curve and that m is the tangent on the point P.

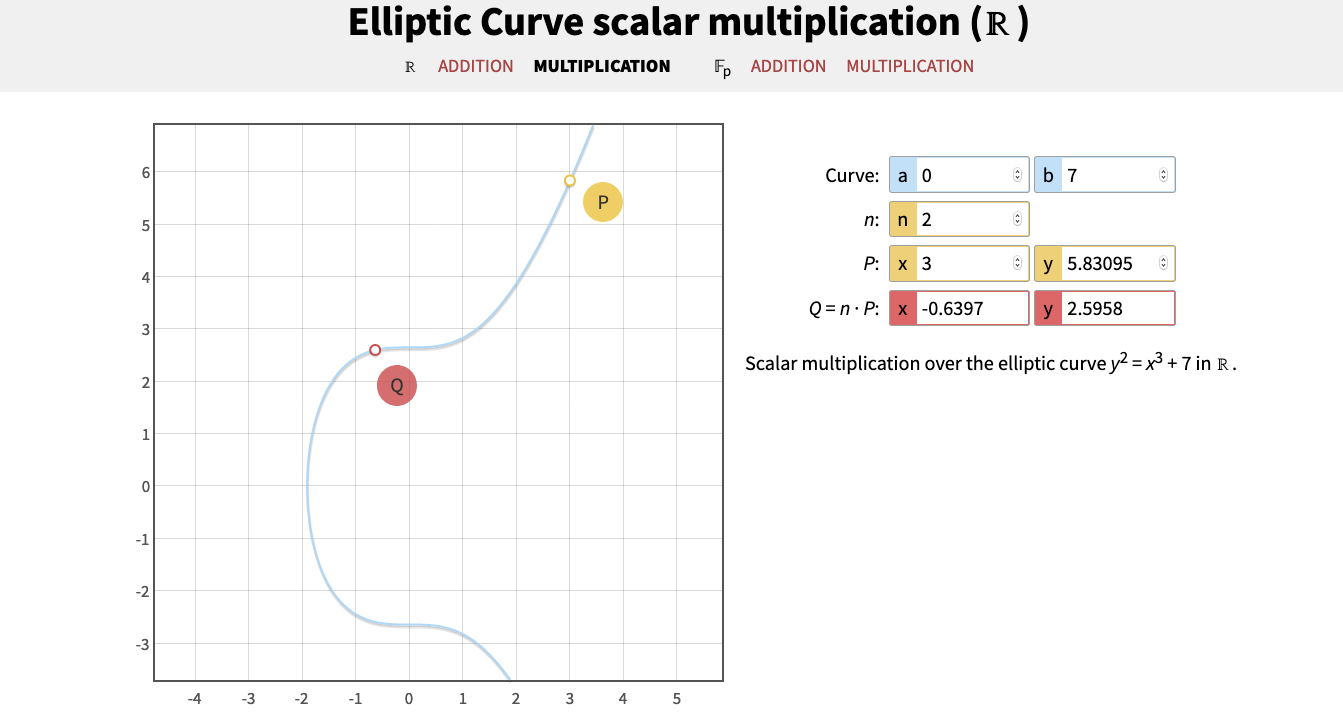
Elliptic curve point multiplication

Elliptic curve point multiplication is the operation of successively adding a point along an elliptic curve to itself repeatedly. It is used in elliptic curve cryptography (ECC) as a means of producing a one-way function. The literature presents this operation as scalar multiplication, thus the most common name is elliptic curve scalar multiplication, as written in Hessian form of an elliptic curve. wikipedia

Point addition and point doubling allow us to define scalar multiplication for elliptic curves such that, xP = R where x is a scalar, P is a point tangent to the curve and R is the resulting point from adding P on to itself x times.

The straightforward way of computing a point multiplication is through repeated addition. However, this is a fully exponential approach to computing the multiplication.

There are several algorithms used to calculate the scalar multiplication:

Elliptic Curve Digital Signature Algorithm (ECDSA)

Bitcoin uses the Elliptic Curve Digital Signature Algorithm (ECDSA) based on elliptic curve cryptography. The particular elliptic curve is known as secp256k1, which is the curve Elliptic curve cryptography (ECC).

\[\displaystyle y^{2} \ =\ x^{3}+7\]

The elliptic curve domain parameters over Fp associated with a Koblitz curve secp256k1 are specified by the sextuple

T = (p,a,b,G,n,h) where the finite field Fp is defined by:

p = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
= 2^256 - 2^32 - 2^9 - 2^8 - 2^7 - 2^6 - 24 - 1
\[\displaystyle The\ curve\ E:\ y^{2} \ =\ x^{3} +ax+b\ over\ Fp\ is\ defined\ by:\] 
a = 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
b = 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000007

The base point G in compressed form is:

G = 02 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798

and in uncompressed form is:

G = 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8

Finally the order n of G and the cofactor are:

n = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141
h = 01

secp256k1 has characteristic p, it is defined over the prime field ℤp. Some other curves in common use have characteristic 2, and are defined over a binary Galois field GF(2n), but secp256k1 is not one of them.

As the a constant is zero, the ax term in the curve equation is always zero, hence the curve equation becomes \(\displaystyle y^{2} \ =\ x^{3}+7\)

Private and Public Keys

A bitcoin wallet contains a collection of key pairs, each consisting of a private key and a public key. The private key (k) is a number, usually picked at random. mastering bitcoin

Private Keys

A private key is simply a number, picked at random. Ownership and control over the private key is the root of user control over all funds associated with the corresponding bitcoin address. The private key is used to create signatures that are required to spend bitcoin by proving ownership of funds used in a transaction. The private key must remain secret at all times, because revealing it to third parties is equivalent to giving them control over the bitcoin secured by that key. The private key must also be backed up and protected from accidental loss, because if it’s lost it cannot be recovered and the funds secured by it are forever lost, too. mastering bitcoin

Generating a private key from a random number

The first and most important step in generating keys is to find a secure source of entropy, or randomness. Creating a bitcoin key is essentially the same as “Pick a number between 1 and \(2^{256}\).” The exact method you use to pick that number does not matter as long as it is not predictable or repeatable. Bitcoin software uses the underlying operating system’s random number generators to produce 256 bits of entropy (randomness). Usually, the OS random number generator is initialized by a human source of randomness, which is why you may be asked to wiggle your mouse around for a few seconds. mastering bitcoin

More precisely, the private key can be any number between 0 and n - 1 inclusive, where n is a constant (n = 1.1578 * 1077, slightly less than \(2^{256}\)) defined as the order of the elliptic curve used in bitcoin. mastering bitcoin

Private Key Wallet import format

1 - Take a private key

0C28FCA386C7A227600B2FE50B7CAE_SAMPLE_PRIVATE_KEY_DO_NOT_IMPORT_11EC86D3BF1FBE471BE89827E19D72AA1D

2 - Add a 0x80 byte in front of it for mainnet addresses or 0xef for testnet addresses. Also add a 0x01 byte at the end if the private key will correspond to a compressed public key

800C28FCA386C7A227600B2FE50B7C_SAMPLE_PRIVATE_KEY_DO_NOT_IMPORT_AE11EC86D3BF1FBE471BE89827E19D72AA1D

3 - Perform SHA-256 hash on the extended key

8147786C4D15106333BF278D71DADAF1079EF2D2440A4DDE37D747DED5403592

4 - Perform SHA-256 hash on result of SHA-256 hash

507A5B8DFED0FC6FE8801743720CEDEC06AA5C6FCA72B07C49964492FB98A714

5 - Take the first 4 bytes of the second SHA-256 hash, this is the checksum

507A5B8D

6 - Add the 4 checksum bytes from point 5 at the end of the extended key from point 2

800C28FCA386C7A227600B2FE50B7CAE11EC8_SAMPLE_PRIVATE_KEY_DO_NOT_IMPORT_6D3BF1FBE471BE89827E19D72AA1D507A5B8D

7 - Convert the result from a byte string into a base58 string using Base58Check encoding. This is the Wallet Import Format

5HueCGU8rMjxEXxiPuD5BDk_SAMPLE_PRIVATE_KEY_DO_NOT_IMPORT_u4MkFqeZyd4dZ1jvhTVqvbTLvyTJ

Sample Java Code

    try {
      // 1 - Take a private key
      String privateKey = "0C28FCA386C7A227600B2FE50B7CAE11EC86D3BF1FBE471BE89827E19D72AA1D";

      // 2 - Add a 0x80 byte in front of it for mainnet addresses or 0xef for testnet addresses.
      // Also add a 0x01 byte at the end if the private key will correspond to a compressed public key
      String privateKeyWIF = "80" + privateKey;

      // 3 - Perform SHA-256 hash on the extended key
      MessageDigest sha256 = MessageDigest.getInstance("SHA-256");
      byte[] sha1 = sha256.digest(DatatypeConverter.parseHexBinary(privateKeyWIF));
      //log.info("Sha1: {}", bytesToHex(sha1).toUpperCase());

      // 4 - Perform SHA-256 hash on result of SHA-256 hash
      byte[] sha2 = sha256.digest(sha1);
      //log.info("Sha2: {}", bytesToHex(sha2).toUpperCase());

      // 5 - Take the first 4 bytes of the second SHA-256 hash, this is the checksum
      String checksum = bytesToHex(sha2).substring(0, 8).toUpperCase();
      //log.info("Checksum: {}", checksum);

      // 6 - Add the 4 checksum bytes from point 5 at the end of the extended key from point 2
      privateKeyWIF = privateKeyWIF + checksum;
      //log.info("Private Key + Checksum: {}", privateKeyWIF.toUpperCase());

      // 7 - Convert the result from a byte string into a base58 string using Base58Check encoding. This is the Wallet Import Format
      privateKeyWIF = Base58.encode(hexToBytes(privateKeyWIF));
      //log.info("Private Key WIF: {}", privateKeyWIF);
    } catch (NoSuchAlgorithmException e) {
      e.printStackTrace();
      return null;
    }

Generating Public Key and Address

0 - Having a private ECDSA key

18e14a7b6a307f426a94f8114701e7c8e774e7f9a47e2c2035db29a206321725

1 - Take the corresponding public key generated with it (33 bytes, 1 byte 0x02 (y-coord is even), and 32 bytes corresponding to X coordinate)

0250863ad64a87ae8a2fe83c1af1a8403cb53f53e486d8511dad8a04887e5b2352

2 - Perform SHA-256 hashing on the public key

0b7c28c9b7290c98d7438e70b3d3f7c848fbd7d1dc194ff83f4f7cc9b1378e98

3 - Perform RIPEMD-160 hashing on the result of SHA-256

f54a5851e9372b87810a8e60cdd2e7cfd80b6e31

4 - Add version byte in front of RIPEMD-160 hash (0x00 for Main Network)

00f54a5851e9372b87810a8e60cdd2e7cfd80b6e31

5 - Perform SHA-256 hash on the extended RIPEMD-160 result

ad3c854da227c7e99c4abfad4ea41d71311160df2e415e713318c70d67c6b41c

6 - Perform SHA-256 hash on the result of the previous SHA-256 hash

c7f18fe8fcbed6396741e58ad259b5cb16b7fd7f041904147ba1dcffabf747fd

7 - Take the first 4 bytes of the second SHA-256 hash. This is the address checksum

c7f18fe8

8 - Add the 4 checksum bytes from stage 7 at the end of extended RIPEMD-160 hash from stage 4. This is the 25-byte binary Bitcoin Address.

00f54a5851e9372b87810a8e60cdd2e7cfd80b6e31c7f18fe8

9 - Convert the result from a byte string into a base58 string using Base58Check encoding. This is the most commonly used Bitcoin Address format

1PMycacnJaSqwwJqjawXBErnLsZ7RkXUAs

Sample Java Code

try {
      // 0 - Having a private ECDSA key 18e14a7b6a307f426a94f8114701e7c8e774e7f9a47e2c2035db29a206321725

      // 1.- Take the Public key
      String publicKey = "0250863ad64a87ae8a2fe83c1af1a8403cb53f53e486d8511dad8a04887e5b2352";

      // 2.-  Perform SHA-256 hashing on the public key. [https://en.bitcoin.it/wiki/SHA-256]
      // The public key will be converted to binary before hashing.
      // This is the way things are hashed internally in bitcoin. (e.g. when creating a transaction ID)
      MessageDigest sha256 = MessageDigest.getInstance("SHA-256");
      byte[] sha1 = sha256.digest(DatatypeConverter.parseHexBinary(publicKey));
      //byte[] s1 = sha256.digest(bitcoinPublicKey.getBytes(StandardCharsets.UTF_8));
      log.info("Sha1: {}", bytesToHex(sha1).toUpperCase());

      // 3.- Perform RIPEMD-160 hashing on the result of SHA-256 [https://en.bitcoin.it/wiki/RIPEMD-160]
      MessageDigest ripeMD160Digest = MessageDigest.getInstance("RipeMD160", "BC");
      byte[] ripeMD = ripeMD160Digest.digest(sha1);
      log.info("RipeMD160: {}", bytesToHex(ripeMD).toUpperCase());

      // 4.- Add version byte in front of RIPEMD-160 hash (0x00 for Main Network)
      byte[] ripeMDExtended = hexToBytes("00" + bytesToHex(ripeMD));
      log.info("RipeMD160Extended: {}", bytesToHex(ripeMDExtended).toUpperCase());

      // 5.- Perform SHA-256 hash on the extended RIPEMD-160 result
      byte[] sha2 = sha256.digest(ripeMDExtended);
      log.info("Sha2: {}", bytesToHex(sha2).toUpperCase());

      // 6.- Perform SHA-256 hash on the result of the previous SHA-256 hash
      byte[] sha3 = sha256.digest(sha2);
      log.info("Sha3: {}", bytesToHex(sha3).toUpperCase());

      // 7.- Take the first 4 bytes of the previous hash SHA-256 hash. This is the address checksum
      String checksum = bytesToHex(sha3).substring(0, 8).toUpperCase();
      log.info("Checksum: {}", checksum);

      // 8.- Add the 4 checksum bytes from stage 7 at the end of extended RIPEMD-160 hash from stage 4. This is the 25-byte binary Bitcoin Address.
      //    byte[] sumBytes = new byte[25];
      //    System.arraycopy(ripeMDExtended, 0, sumBytes, 0, 21);
      //    System.arraycopy(sha3, 0, sumBytes, 21, 4);
      String ripeMDExtendedAndChecksum = bytesToHex(ripeMDExtended) + checksum;
      log.info("RipeMDExtended + Checksum: {}", ripeMDExtendedAndChecksum.toUpperCase());

      // 9.- Convert the result from a byte string into a base58 string using Base58Check encoding. This is the most commonly used Bitcoin Address format
      //bitcoinAddress = Base58.encode(sumBytes);
      String address = Base58.encode(hexToBytes(ripeMDExtendedAndChecksum));
      log.info("Address: {}", address);
    } catch (NoSuchAlgorithmException e) {
      e.printStackTrace();
    } catch (NoSuchProviderException e) {
      e.printStackTrace();
    }

The source code can be found on github. bitcoin-keypair-generator-sample

References